Home • Up
MDAG.com Internet Case Study 26
Scaling and Equilibrium Concentrations
in Minesite-Drainage Chemistry
by K.A. Morin and N.M. Hutt
© 2007 Kevin A. Morin and Nora M. Hutt
(An excerpt from the upcoming book, Minesite Drainage Chemistry)
Click here for a PDF version of this MDAG.com Internet Case Study 26
Abstract
In this case study, we present various facets of scaling for minesite-drainage chemistry, to
reinforce the lesson that “Many people say they already know how to scale minesite-drainage
chemistry, but no one actually understands scaling well”. Considerable discussion is given on the
quantitative “scale transition” at which minesite-drainage chemistry switches between kinetic
controls and equilibrium controls.
A generic conceptual model was developed for the microscale, mesoscale, and full scale.
This showed, for all scales, that physical aspects like water flowpaths, sequences of minerals, and
sampling location affect drainage chemistry. One example on the microscale of pores showed how
variable chemistry could be over short distances, and that various averaged concentrations and rates
over the pore network did not agree. Also, acid-base accounting and laboratory kinetic tests on a
larger scale implicitly predict homogenized conditions, which do not apply to full-scale minesite
components.
In this case study, “equilibrium” encompasses thermodynamic equilibrium, metastable
equilibrium, dynamic equilibrium, pseudo-equilibrium, and emergence, which allow aqueous
concentrations to rise to a certain level and no higher. Increases in scaling factors like volume,
kinetic rate, residence time, and solid:liquid ratio cause aqueous concentrations to increase, until a
maximum equilibrium level is attained.
The “scale transition” represents the general break between kinetically determined and
equilibrium determined concentrations in mg/L. Examples showed that the scale transition for near-neutral copper leaching could require as little as 40 kg, or as much as 40 tonnes of rock or tailings.
These weights translated into vertical heights of 2 cm to 20 m for rock or tailings. Short heights like
2 cm explain why control options like soil covers and permafrost often do not lower aqueous
concentrations substantially. In fact, reduction in infiltration by a soil cover increases the likelihood
of maximum equilibrium concentrations in drainage. Generic equations were provided for
calculating scale transition as a weight or height, requiring a kinetic rate and an equilibrium
concentration as input.
Although small-scale 1-kg laboratory kinetic tests like humidity cells are specifically
designed with high dilution, sometimes the leaching rate of a particular element can be so high that
equilibrium is attained. This is more typical at acidic pH, but has also been seen at near-neutral pH.
In these cases, the concentrations from cells in mg/L are direct predictors of full-scale chemistry.
Therefore, these equilibrium concentrations cannot be used as kinetic rates (a) to predict when a
sample might become acidic or (b) to calculate a criterion for Net Potential Ratio to identify net-acid-generating material.
The accumulation of secondary minerals, when equilibrium concentrations are achieved, can
greatly extend the length of time that equilibrium concentrations persist. This is due to the
subsequent dissolution of the accumulated minerals.
Full-scale equilibrium chemistry at minesites has been defined by Empirical Drainage
Chemistry Models (EDCMs), which typically require at least several hundreds of analyses for
statistical validity. EDCMs showed that average annual equilibrium values and their seasonal
variabilities repeated year after year, as long as “master” parameters like pH remained relatively
constant. Thus, full-scale equilibrium is not one constant concentration throughout the year. In fact,
seasonal variability of equilibrium concentrations exceeded one order of magnitude for some
elements. Also, seasonal variability and average annual concentrations were unique for each
element at each minesite.
Table of Contents
1. Introduction
2. Objective
3. Observations on Scale for Geochemical Predictions
3.1. Microscale Observations of Minesite-Drainage Chemistry
3.2. Mesoscale Observations of Minesite-Drainage Chemistry
3.3. Full-Scale Observations of Minesite-Drainage Chemistry
4. Scale Dependency and Equilibrium of Aqueous Concentrations
5. Various Scales of Testwork for Predicting Minesite Drainage Chemistry
6. Accumulation of Secondary Minerals
7. Full-Scale Equilibrium
8. Conclusion
9. References
1. Introduction
In our MDAG Internet Case Studies 3, 7, and 23 (Morin and Hutt, 1998a, 1998b, and 2006),
we addressed drainage-chemistry aspects of scale, kinetics vs. equilibrium, repeating patterns, and
grain size. In this case study, we carry the analysis further, into quantitative aspects of scale
transitions, weights and thicknesses of mined materials, and predictions of concentrations.
For minesite-drainage chemistry, one of the greatest challenges is adjusting predictions from
small-scale samples to full-size minesite components, such as mined-rock piles, tailings
impoundments, and mine walls. Many have discussed the implications of scale on geochemical
predictions. For example, Hornberger and Brady (1998) considered a ship in a bottle.
“The differences in scale between the backfilled surface mine site and the typical kinetic test
apparatus are many orders of magnitude apart. . . . Actually, while it is possible to construct
a replica of a ship in a bottle, it is improbable that the conditions of a stratified surface mine
backfill can be replicated in a test tube or even the average sized leaching column.”
As another example, Petrunic and Al (2005) indicated a tailings porewater sample spanning a depth
of several centimeters can “oversimplify” (homogenize) small-scale geochemical variations. More
generally, Anderson (1972) explained,
“The constructionist hypothesis breaks down when confronted with the twin difficulties of
scale and complexity. . . . At each level of complexity entirely new properties appear . . .
We can now see that the whole becomes not merely more, but very different from the sum
of its parts.”
There is no doubt that scale and corresponding complexity are important to predictions of
drainage chemistry. For example, Morin and Hutt (2000a) showed how a mined-rock pile,
containing 300 times more neutralization potential (NP) than acid potential (AP) (NP/AP = Net
Potential Ratio = NPR = 300), could still release acid rock drainage (ARD) along some flowpaths.
This violates common ARD prediction rules for small samples. Instead of the bulk NPR ratio,
Morin and Hutt (2000a) showed the important predictive parameter was the physical distance
separating units of net-acid-generating rock. This shows that physical factors can be critical in
large-scale geochemical predictions.
Expert reviewers have provided comments on our past work with scaling. The major lesson
we learned from them was, “Many people say they already know how to scale minesite-drainage
chemistry, but no one actually understands scaling well”. The former part of the lesson was stated
by the reviewers, but the latter was seen in their comments. The following should be humbling, and
will reinforce that lesson.
2. Objective
This MDAG case study discusses geochemical aspects of scale, highlighting issues affecting
the understanding and prediction of minesite-drainage chemistry. There is a particular focus on the
“scale transition” at which geochemical predictions change from kinetic to equilibrium conditions.
3. Observations on Scale for Geochemical Predictions
This section develops a conceptual model for understanding and predicting minesite-drainage
chemistry on various scales. Figure 1 presents a simplified, generic sample of rock or tailings. This
sample is heterogeneously composed of various acid-generating, acid-neutralizing, and leachable
minerals, depicted as individual boxes of varying colours or shades. Each box represents the
smallest indivisible, homogenous unit in the conceptual model, sometimes called “grain” in scaling
studies (e.g., Wu, 1999; Wu and Li, 2006).
An important point about Figure 1 is that it is meant to be generic, three dimensional, and
a composite through time. One reviewer told us Figure 1 was not valid, because flowpaths crossed.
Thus, that reviewer considered Figure 1 to be a saturated porous medium depicted at one point in
time. It could just as well be an unsaturated coarse waste-rock pile, where flowpaths flowed one
way over the back end of a boulder one day, and the opposite way over the front end of the same
boulder the next day. Figure 1 is much like a Rorschach Inkblot Test - it reveals your preconceived
notions of scaling. Stare at Figure 1 closely and abandoned preconceived notions, if you want to
reach scaling nirvana.
3.1. Microscale Observations of Minesite-Drainage Chemistry
In Figure 1, the length of scale, labelled “L”, is generally micrometers to centimeters for the
microscale. Connected pore spaces allow water and air to pass through the sample, producing
distinct fluid flowpaths. Some flowpaths may merge and diverge in irregular patterns over time.

Figure 1. Schematic diagram of adjoining blocks of differing chemical composition, with flowpaths
for water and air (pore spaces may be filled with air and/or water).
The chemistry and pH of water passing over the surface of any one particle will reflect the
aqueous chemistry and pH created by the preceding particles, modified by the geochemical
reactivity of the current particle. For example, pH may fluctuate among acidic, near-neutral, and
alkaline values as water moves along an internal flowpath (Zone 2 in Figure 1). This can only be
observed if the water is extracted at distinct points within the sample. However, if extracted
internally, its geochemical evolution ceases and it may not represent the sample’s effluent (Zones
3 to 5). The chemistry and pH of a flowpath as it immediately exits the sample (Zone 3) will reflect
both the number and the sequence of contacted acid-generating, acid-neutralizing, and leachable
minerals, as well as environmental conditions such as Eh.
This shows that on a microscale the understanding and the prediction of drainage chemistry
are not simple or easy. Physical aspects like water flowpaths, sequences of minerals, and sampling
location affect drainage chemistry. For better or worse, this scale is often simplified by considering
the next larger scale at which most laboratory testwork is conducted (Section 3.2).
Some have looked closely at geochemical reactions and evolving drainage chemistry in a
microscale network. For example, Li et al. (2006) conducted “pore-scale network modelling”. The
three-dimensional network simulated a consolidated sandstone with 10% reactive pores gathered
in clusters, a total of 9000 pores (30 x 10 x 30), and a total volume of 5.0 x 1.7 x 5.0 mm. Kinetic
reaction rates of anorthite and kaolinite were based on aqueous H+, OH-, and degree of
undersaturation or supersaturation, within acidic pore water created by high-pressure CO2 levels.
Laminar flow, equilibrium reactions for many aqueous species, and diffusion of aqueous species
among pores were included. Mineral precipitation was allowed only in “reactive” pores already
containing anorthorite or kaolinite.
Based on the pore-scale network, three normalized reaction rates for anorthite and kaolinite
were defined. The rates were differentiated by the choice of how H+, OH-, and the degree of
undersaturation-supersaturation were calculated.
1) Network reaction rate (RN) is the sum of rates within each reactive pore based on individual pore
chemistry, divided by the mineral surface area in all reactive pores. This ignores any
concentrations in the non-reactive pores.
2) Continuum-scale reaction rate (RC) is the overall rate based on assuming the pore network is a
continuum with one concentration each of H+ and OH- throughout. As a result, RC is not
weighted by, or variable with, pore size.
3) Volume-averaged reaction rate (RʹN) is the overall rate based on the sums of H+ and OH- in all
non-reactive and reactive pores divided by the volume of all pores across the pore network.
Thus, RʹN is weighted by pore size, which simulates a water sample from the entire pore
network drawn into a monitor well. However, Zones 3 to 5 in Figure 1 include contact with
all grains along a flowpath, whereas RʹN assumes the water is drawn instantaneously from
all pores without the opportunity for the water to react with other grains. Also, cyclical
flushes of humidity cells dilute pore chemistry in Zone 2, but allow the homogenized
chemistry to contact most grains for some time, leading to a variation on Zone 5 results.
The pore-scale modelling by Li et al. (2006) showed that spatial variations in reaction rates
and aqueous concentrations varied by orders of magnitude among the pores. This was accompanied
by pH variations of more than 0.5 pH units (Figures 2 and 3). Thus, single-value representations
(RC and RʹN, Figure 3) can introduce large errors and scaling effects that appear to contradict
mineral-specific rates. Also, thermodynamic equilibrium that applied in specific pores was distorted
when averaged over the pore network, so that another, distorted “metastable” equilibrium appeared
on a larger scale.

Figure 2. Two-Dimensional Map of Aqueous pH within One Plane of a Three-Dimensional Pore-Scale
Network, with Water Flowing from Left to
Right and Only Ten Percent Reactive Pores (see text and
Figure 3) for additional details, adapted from Li et al., 2006).

Figure 3. Histograms of pH within All Pores (top), Only Non-Reactive
Pores (middle), and Only Reactive Pores (bottom) from a
Three-Dimensional Pore-Scale Network (see text and Figure 2 for
additional details, adapted from Li et al., 2006).
3.2. Mesoscale Observations of Minesite-Drainage Chemistry
Hand-sized and intermediate-sized (“mesoscale”) samples have lengths (L in Figure 1) of
centimeters to meters. Predictions for this scale, based on tests like acid-base accounting (ABA),
are typically checked against results of similarly scaled kinetic tests like humidity cells and leach
columns.
In the schematic diagram of Figure 1, kinetic tests on this scale are often sampled at Zone
5. Therefore, ABA has been calibrated over the years to mesoscale samples of a composited
hydrologic/hydrogeologic system at Zone 5. Where flowpaths have been captured separately (e.g.,
Zones 3 and 4), significant fluctuations in chemistry with time and location have been seen (e.g.,
Beckie et al., 2005; Li, 1999). Therefore, monitoring or predicting drainage chemistry in Zones 2
through 4 is not easily accomplished with mesoscale data from Zone 5.
3.3. Full-Scale Observations of Minesite-Drainage Chemistry
Figure 1 remains a valid analogue even on the full scale of a minesite component, with the
scale (L in Figure 1) roughly tens to thousands of meters. In this case, Zone 2 in Figure 1 represents
a waste-rock pile, tailings impoundment, low-grade-ore stockpile, or wall of an underground or
open-pit mine. Piezometers, for example, can extract water from various locations within Zone 2.
Morin and Hutt (1997, 2000a, and 2001) showed a similar, less generic diagram for a full-scale
mined-rock pile, including a water table and lateral seepage.
At this scale, Zones 3 to 5 represent drainage into the surrounding surface watercourses and
the surrounding groundwater systems, which are the typical targets for full-scale predictions.
Therefore, when comparing smaller-scale samples (Sections 3.1 and 3.2) to full-scale field samples,
it is critical to know from which Zones all samples were collected.
This explains the findings of Kempton et al. (1997), Mehling et al. (1997), and Morin and
Hutt (2000a). For example, the probability of having one flowpath at Zone 3 being acidic would not
be dependent on the overall NP/AP ratio of the entire component. Instead, it would depend on the
amounts and sequences of acid-generating and acid-neutralizing blocks encountered by each
flowpath (Figure 1). As a result, Morin and Hutt (2000a) found that a rock-pile-wide NPR ratio of
300:1 could still release some ARD. Kempton et al. (1997) also showed that release of ARD can
be affected by the random distribution of net-acid-generating rock in a pile. This work highlights
the importance of factors like water movement, geology, and sequence of mining in correctly
predicting drainage chemistry at the full scale.
Other factors can cause drainage chemistry to change substantially only downstream of the
component, after the drainage enters Zones 3, 4, and 5 (Figure 1), and thus violating predictions
from Zone 2 or from smaller scales. These factors include oxidation and precipitation of iron,
oxidation of thiosalts, interactions with substrate materials including ion exchange, and daily
fluctuations in downstream temperature and sunlight (e.g., Dinardo, 2003; Jones et al., 2004, Shope
et al., 2006, and Morin, 2003).
Morin and Hutt (1997, 1999) found that seasonal fluctuations between acidic and
near-neutral pH from one mined-rock pile were due to seasonal fluctuations of flow from different
sources rather than geochemistry. Downstream flow (Zone 5 in Figure 1) was relatively high from
the ARD-releasing pile during some seasons (one flowpath in Zone 3), and relatively high from an
adjacent, large near-neutral pond during other seasons (another flowpath in Zone 3). Downstream
monitoring gave the impression that pH from the pile was fluctuating substantially, when in fact, the
variable flow rates from the two flowpaths explained the Zone 5 variability. Such flowpath effects
on drainage chemistry have also been seen in composite portal flows from underground mines
(Morin and Hutt, 1997 and 2001).
Therefore, while Figure 1 is rudimentary in nature, it explains why some drainage-chemistry
predictions have failed and how geochemical predictions at the full scale are only partly dependent
on geochemistry.
4. Scale Dependency and Equilibrium of Aqueous Concentrations
The preceding subsections explained that scale, physical factors, mining sequence, and
monitoring points along flowpaths can greatly affect the assessment and prediction of minesite-drainage chemistry. This section examines in more detail the effect of scale on aqueous
concentrations in mg/L.
In this paper, “equilibrium” encompasses thermodynamic equilibrium, metastable
equilibrium, dynamic equilibrium, pseudo-equilibrium, and emergence. Emergence can generally
be defined as the appearance of distinct patterns or properties as scale increases, due to self-organization in complex systems, or “the whole becomes not merely more, but very different from
the sum of its parts” (Anderson, 1972).
Under this general concept of equilibrium, aqueous concentrations can rise to a certain level
and no higher (Figure 4 and Section 7). From the perspective of scale, this means simplistically that
the aqueous concentrations appearing in Zones 2 to 5 will rise as the volume of mine material
increases (that is, as L in Figure 1 increases. At some point (the “scale transition”), some maximum
concentration is achieved and rises no higher. Similarly, as other scaling factors increase, like
kinetic rate and residence time and solid:liquid ratio, a maximum equilibrium level will again be
attained. Thus, the scale transition represents the general break between kinetically determined and
equilibrium determined concentrations in mg/L.

Figure 4. The Conceptual Model for Scaling Minesite-Drainage Chemistry
through Kinetic and Equilibrium Conditions, including Components
of Scale.
To be accurate, it is important to understand that scaling is also dependent on aspects like
the observer and the density and frequency of sampling (Wu, 1999; Wu and Li, 2006). For example,
humidity cells are often rinsed weekly, but scaling effects can be major and unpredictable if the
weekly rinses are analyzed only biweekly (Morin and Hutt, 2007).
A critical aspect of drainage-chemistry predictions at minesites is identifying the scale at
which the scale transition is met and surpassed. Does the transition often require just kilograms,
tonnes, or millions of tonnes of rock or tailings? To answer this, we start with a specific example
and then derive a general answer.
At near-neutral pH, the International Kinetic Database (Morin and Hutt, 1997 and 2001;
www.mdag.com/ikd.html) shows that a copper-leaching rate of 0.0005 mg/kg/wk is among the
lowest measured values and 0.05 mg/kg/wk is among the highest measured (Figure 5). If a minesite
component could produce a maximum equilibrium copper concentration of 1 mg/L, how many
tonnes of rock, over a 1 m2 lateral area, would be needed to reach the scale transition? Figure 6
graphically portrays this question, using both a relatively high and low infiltration rate (1.0 and 0.1
m3/m2/yr).
The detailed answer is as follows (Figure 7). At one of the highest near-neutral copper-leaching rates and with relatively low infiltration and dilution, the scale transition and equilibrium
concentration can be reached with 0.04 t (40 kg) of near-neutral, fine-grained, well-aerated, well-flushed rock or tailings. The other extreme with a very low leaching rate, and high infiltration and
dilution, is 40 t.

Figure 5. Range of Copper Leaching Rates from the International
Kinetic Database, including Two Extreme Rates at Near-Neutral
pH.
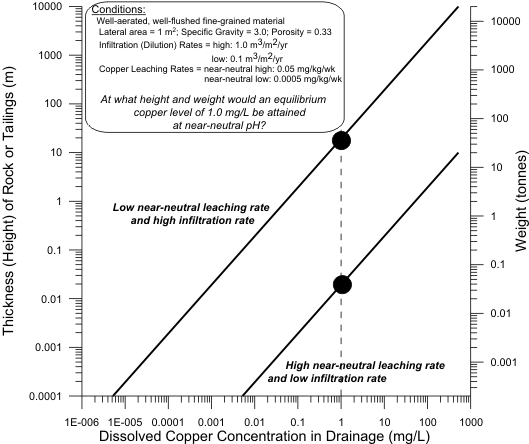
Figure 6. Simplified Example to Calculate Tonnage and Height of Rock or
Tailings
Needed to Reach an Equilibrium Copper Concentration of 1 mg/L at
Various
Rates of Copper Leaching and Infiltration.

Figure 7. Simplified Example Showing Only 0.04-40 t of Rock or Tailings, or
0.02-20 m Height, Needed to Reach an Equilibrium Copper Concentration
of 1 mg/L.
The preceding “fine-grained, well-aerated,
well-flushed” conditions are also scaling factors, which are addressed below.
Also, if conditions were acidic rather than near neutral as in this example,
then the scale-transition tonnage would typically be orders of magnitude less,
because acidic rates of copper leaching are typically orders of magnitude higher
(Figure 5).
Based on a specific gravity of 3.0 and a porosity of 33%, the scale-transition tonnage can be translated into a height of material over a 1 m2 lateral area (left side of Figures 6 and 7). For the preceding extreme copper examples, heights as little as 0.02 m (2 cm) or as much as 20 m can represent the scale transition. This explains some apparent geochemical surprises for drainage-chemistry-control options, like soil covers and permafrost.
- Soil cover: A soil cover can reduce infiltration and thus lower the scale-transition height so that an equilibrium concentration is attained with less thickness of mined material. A soil cover may also reduce air entry. However, little air would be needed to oxidize the required outermost layer of mined material (perhaps much less than 1 m, especially if acidic) and maintain the equilibrium concentration in the basal drainage. Thus, after the installation of a soil cover, drainage flow can decrease, but chemistry would not change substantially. This is a common observation.
- Permafrost: The uppermost “active layer” that thaws in permafrost each summer is often around one meter or more. That thickness can be sufficient to create equilibrium concentrations in drainage waters. This is one reason why permafrost cannot stop metal leaching or ARD.
The preceding example can be generalized for more robust predictions of the scale transition,
for many elements, under various environmental conditions. First, Figure 7 can be standardized to
a single infiltration rate of 1 m3/m2/yr to calculate the required tonnage over a 1 m2 lateral area,
leading to Figure 8. To be clear, the kinetic rate and the equilibrium concentration for an element
must be known in advance to use Figure 8. If a minesite component had an infiltration rate of only
0.1 m3/m2/yr, then one-tenth the tonnage indicated by Figure 8 would be needed to reach the scale
transition and equilibrium concentration:
Required Weight to Reach Equilibrium (in t/m2 lateral area) =
Required Weight from Figure 8 * Infiltration (in m3/m2/yr) (Eq. 1)
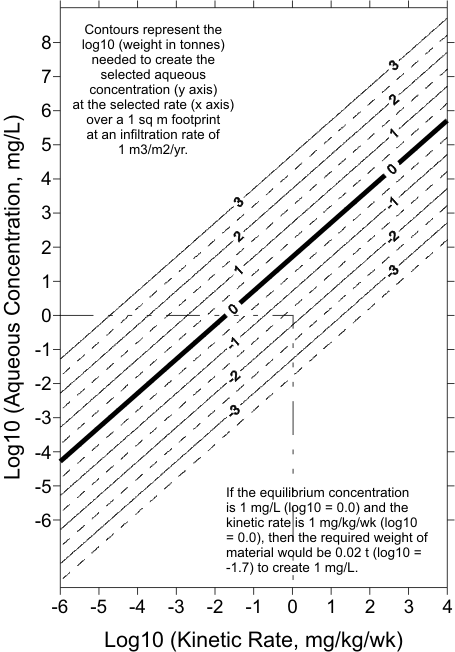
Figure 8. Generalized Estimation of the Weight Required to Reach a
Specified Aqueous Equilibrium Concentration at a Specified
Kinetic Rates, using Log10 Values and Normalized to an
Infiltration Rate of 1 m3/m2/yr.
However, there are other scaling factors. For example, kinetic rates are often obtained from
humidity-cell samples that are usually fine grained, well aerated, and well flushed. In a full-scale
component, only 10% of the material might be fine grained like a humidity cell, so ten times more
weight of the component would be needed to reach the scale transition. The same applies to a fine-grained component in which only 10% of the grains are flushed regularly by infiltration.
Therefore, the generic equation to predict the weight to reach scale transition, above which
equilibrium concentrations can be expected, is:
Required Weight to Reach Equilibrium (in tonnes/m2 lateral area) = (Eq. 2)
[Equilibrium Concentration (in mg/L) * Infiltration (in m3/m2/yr)] /
[Kinetic Rate (in mg/kg/wk) * 52 *(% of fine-grained, well-flushed, and well-aerated material/100%)]
The generic equation for the corresponding height of material to reach the scale transition
is:
Required Height to Reach Equilibrium (in m, or m3 over a 1 m2 lateral area) = (Eq. 3)
Required Weight from Equation 2 / [Specific Gravity * ((100- % porosity) / 100%)]
Although the preceding paragraphs discussed the scaling of aqueous concentrations in mg/L,
another issue is the scaling of rates (mg/kg/wk) for the case when scale transition is not encountered
even at full scale. Do rates experience scaling effects like concentrations? How could full-scale
rates in a heterogenous minesite component be measured?
There are major discrepancies in kinetic rates between various scales and conditions, even
for a single mineral (e.g., Morin and Hutt, 1997 and 2001). Without explaining scale discrepancies,
some studies have attempted to measure full-scale reaction rates, which are no doubt spatially
variable, at distinct point locations within Zone 2 of Figure 1. Preceding discussions have
highlighted the potential complexities of such aqueous interpretations along pathways of Zone 2;
the same holds for interpretations of rates. Nevertheless, various authors have reported bulk reaction
rates based on (1) aqueous chemistry that may be affected by equilibrium, (2) oxygen transport and
consumption requiring assumptions, like air movement only by diffusion or simplistic large-scale
air movement in one or two dimensions, (3) heat/temperature patterns that are affected by variable
thermal conductivities of rock, tailings, water, and air, and by any convection of air, and (4) intrinsic
oxidation rates spanning a narrow range of values based on one or more of the preceding points
(e.g., Garvie et al. 1997, Ritchie, 1995; Kuo and Ritchie, 1999).
Therefore, in our opinion, reliably measuring and comparing bulk reaction rates on various
scales up to the full-scale minesite component is not currently possible. In fact, an alternative
approach is to assume that full-scale “rates” are limited by equilibrium (Figure 4). As a result, the
subtraction of these full-scale “rates” from small-scale rates provides an estimate of the
accumulating secondary minerals within a component (see Section 6).
5. Various Scales of Testwork for Predicting Minesite Drainage Chemistry
At least some elements in full-scale minesite drainages frequently attain equilibrium (Section
7; Morin and Hutt, 1997 and 2001). Where this is expected, an important issue is whether
smaller-scale kinetic tests can yield reliable predictions of those full-scale equilibrium
concentrations. For fine-grained, well-rinsed, and well-aerated kinetic tests, like humidity cells
discussed in Section 4 (Hanna and Brant, 1962; Morin and Hutt, 1997, 2001), the intent of the
testwork is not to obtain equilibrium concentrations. It is to obtain unit-weight reaction rates and
NP/AP consumption rates without distortion by equilibrium constraints. For these tests, the
theoretical answer is “no” - they should not provide reliable estimates of full-scale equilibrium
concentrations on a mg/L basis.
On the other hand, other kinetic tests more likely attain equilibrium, like non-Sobek
drip-leach humidity cells and leach columns, would not provide reliable estimates of reaction rates.
If their aqueous concentrations are shown to exceed the scale transition (Section 4), then they can
provide estimates of full-scale equilibrium concentrations, especially when water is continuously
recirculated to increase residence time (Figure 4). The equilibrium concentrations from these small-scale kinetic tests can be considered predictions for the full scale, if relevant physical, chemical, and
biological conditions are similar in the tests and in the minesite component. Demonstrating this can
be an onerous and uncertain task (see the ship-in-the-bottle quotation at the beginning of this case
study).
Although the operation of well-rinsed humidity cells is intended to avoid equilibrium
concentrations, we have found that equilibrium can be achieved for some elements. In one case of
an existing, strongly acidic minesite, several scales of kinetic testing showed that well-rinsed 1-kg
humidity cells provided aqueous pH and dissolved-iron concentrations that generally matched
full-scale concentrations (Figures 9 and 10; the vertical bars for various scales of testwork overlap
in the figures to show similarities and differences). In fact, the corresponding larger-scale kinetic
tests sometimes predicted lower pH and overestimated dissolved iron, and thus the 1-kg cells were
the best predictors. Nevertheless, for some elements like dissolved zinc, the small-scale cells did
not reach the applicable scale transition and thus underestimated full-scale equilibrium
concentrations (Figure 11). For this reason, 1-kg humidity cells can sometimes extend above the
scale transition (Figure 12), but do not always do so for all elements.

Figure 9. Example of Aqueous pH from a 1-kg Humidity Cell Generally Matching
pH at the Full-Scale Minesite, Indicating the Scale Transition Had Been
Attained with 1 kg of Material (see also Figures 10 and 11).

Figure 10. Example of Dissolved Iron from a 1-kg Humidity Cell (in mg/L)
Generally Matching Dissolved Iron at the Full-Scale Minesite, Indicating the
Scale Transition Had Been Attained with 1 kg of Material (see also Figures 9
and 11).
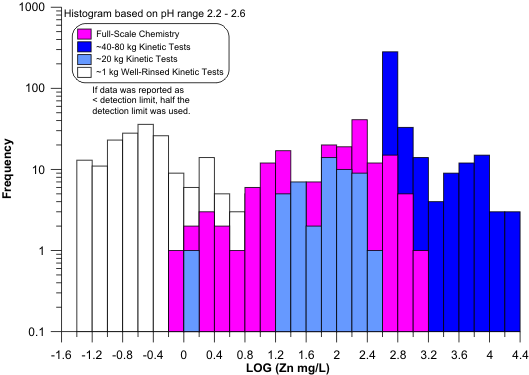
Figure 11. Example of Dissolved Zinc from a 1-kg Humidity Cell (in mg/L)
Underestimating Dissolved Zinc at the Full-Scale Minesite, Indicating the
Scale Transition Had Not Been Attained with 1 kg of Material (see also
Figures 9 and 11).
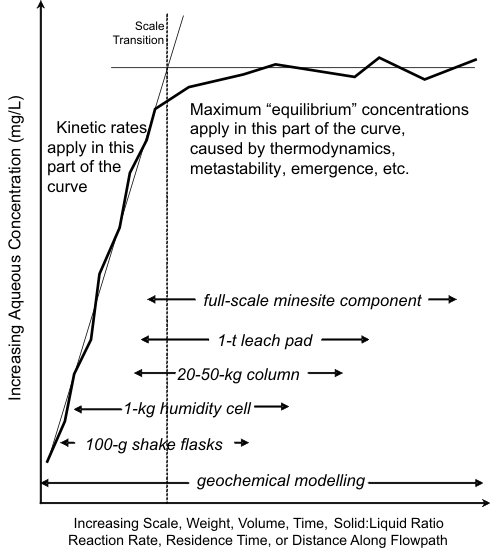
Figure 12. The Conceptual Model for Scaling Minesite-Drainage Chemistry,
with General Ranges of Scale for Various Types of Geochemical
Testwork
and Models.
For the
preceding minesite, 1 kg of sample produced roughly the same pH and aqueous
concentrations of some elements as 109 kg, which highlighted major implications for site-specific
mitigation options. For example, if elimination of oxygen was needed to control chemistry, virtually
every kg had to be thoroughly isolated to lessen drainage concentrations substantially. This could
have important implications for mitigation costs (e.g., Morin and Hutt, 2006b).
In another example, 1-kg cells from a relatively dilute, near-neutral minesite produced
maximum dissolved molybdenum concentrations of 1.5 mg/L. In comparison, a 20-tonne on-site
leach test of the same rock unit, which was 20,000 times more massive, produced up to 4.5 mg/L.
Furthermore, a 60,000 t waste-rock pile produced up to 4.5 mg/L, and more than 2 km of
underground workings produced up to 4.5 mg/L at the portal. Thus, the maximum cell
concentrations were close to the full-scale concentrations at near-neutral pH, in this case due to the
solubility of powellite (CaMoO4). This meant that maximum cell concentrations had exceeded the
scale transition for molybdenum at this site.
In the two preceding examples, the use of kinetic rates (mg/kg/wk) for those elements at
equilibrium would lead to predictive errors. Assessments of equilibrium concentrations in small-scale laboratory tests are rarely reported based on our experience. Therefore, the indiscriminate use
of small-scale concentrations and corresponding rates, without consideration of the scale transition,
is a source of drainage-chemistry prediction error.
Also, the delineation of NPR criteria for a rock unit or minesite, based on laboratory kinetic
tests that surpassed the scale transition for sulphate and calcium, can be wrong. For example, a
minesite has an NPR criterion of 1.5, so that all rock less than 1.5 is net acid generating. If kinetic
tests reach equilibrium causing the precipitation of secondary gypsum, then the tests can incorrectly
report that the NPR criterion was actually 4.0 or higher. Thus, much more rock would be incorrectly
predicted as net acid generating (Morin and Hutt, 1998c).
As an interesting footnote, some heap-leach models reportedly do not include equilibrium,
and thus simulate leaching as a purely kinetic process (Jansen and Taylor, 2002).
Laboratory-measured rates are then scaled up by a simple factor, such as dividing the laboratory rate
by 1.5 to estimate the full-scale rate. As a result, an arbitrary scaling factor and the unexpected
attainment of equilibrium with scale (Figure 4) could lead to erroneous full-scale predictions from
such heap-leach models.
6. Accumulation of Secondary Minerals
It is important to understand that solid-liquid interactions do not stop at equilibrium. Instead,
because equilibrium often reflects mineral solubility, primary minerals can continue dissolving and
secondary minerals can continue precipitating at the same rate. As a result, net equilibrium
concentrations do not change substantially. However, the ongoing accumulation of secondary
minerals has important implications on scale. In a general sense, accumulated secondary minerals
show that minesite components, as complex systems, have “memory” or hysteresis, by which past
processes can affect current and future conditions.
Where secondary minerals accumulate, minesite-drainage chemistry can pass through three
stages (Figure 13). The First Stage is primary reaction and leaching, when secondary minerals
accumulate under equilibrium conditions. When the primary minerals are exhausted, the chemistry
enters the Second Stage.

Figure 13. Three Stages of Minesite-Drainage Chemistry Where Secondary
Minerals Accumulate.
Because the secondary minerals accumulated under equilibrium, they begin dissolving to
maintain equilibrium in the Second Stage, accounting for the “memory” of past aqueous
concentrations. When most of the secondary minerals are dissolved, aqueous concentrations
decrease in the Third Stage, also moving left on Figure 4 and perhaps below the scale transition into
kinetic controls.
As a result, the duration of equilibrium concentrations through the First and Second Stages
is determined by a complex set of primary and secondary geochemical reactions, as well as climate,
flowpaths, and mineral sequences as discussed above. As a general rule-of-thumb, the Second Stage
can last ten times longer than the First Stage. An important exception is underwater disposal of
material in the First Stage, upon which soluble accumulated minerals are dissolved quickly and the
Second Stage may be less than a year. Full-scale case studies of this exception confirmed the large,
rapid escalation of some aqueous concentrations.
7. Full-Scale Equilibrium
Again, it is important to recognize that solid-liquid interactions do not stop at equilibrium.
However, net equilibrium concentrations are depicted as a relatively steady horizontal line in Figure
4. In reality, variable pH, Eh, chemical activities, geochemical buffer points, seasonal climatic
conditions, and site-specific factors cause equilibrium concentrations to vary spatially and
temporally.
Since equilibrium can be seen at full-scale minesites, is it one exact number that persists at
all times? If not, how variable can equilibrium be? What does full-scale equilibrium at a minesite
look like?
Empirical Drainage Chemistry Models (EDCMs) have quantitatively explained full-scale
equilibrium (Morin and Hutt, 1993, 1997, 2000b, and 2001; Morin, 1994; Morin et al., 1993, 1995a,
1995b, and 2001; Day et al., 1996). Several publications showed that, if pH or sulphate was
relatively steady, annual means and annual standard deviations of drainage chemistry repeated year
after year, for several years to as much as 25 years. In other words, equilibrium concentrations were
dependent on certain “master” parameters like pH, whose effect must be filtered out before defining
or predicting equilibrium. However, several hundreds to thousands of water analyses are needed
for a statistically valid EDCM.
EDCMs contain “best-fit” lines that define average annual equilibrium concentrations (left
sides of Figure 14 and 15, and Table 1). At any particular pH, the vertical spread of aqueous
concentrations can resemble a lognormal distribution (right sides of Figures 14 and 15, and Table
1) and define a standard deviation in logarithmic cycles. High-frequency (every four hours)
sampling, and comparisons of year-to-year analyses, showed that the standard deviations (vertical
spread) generally repeated year after year. Thus, they did represent seasonal variability in
equilibrium concentrations.
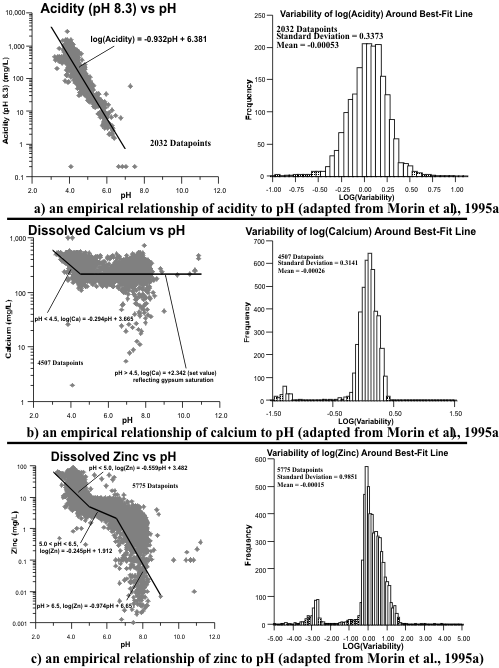
Figure 14. Examples of Empirical Drainage-Chemistry Correlations with pH.

Figure 15. Examples of Copper vs. pH Correlations at Three Minesites.
Table 1. An Example of an Empirical Drainage-Chemistry Model
Including an Open Pit, Several Waste-Rock Dumps, and a Tailings Impoundment
(adapted from Morin et al., 1995b)
|
Parameter
|
pH Range
|
Best-Fit Equation
|
Log(Std Dev)
|
Acidity
|
pH < 3.5
|
log(Acid) = -0.932pH +5.864
|
0.345
|
pH > 3.5
|
log(Acid) = -0.360pH + 3.862
|
Alkalinity
|
pH > 4.5
|
log(Alk) = +0.698pH - 3.141
|
0.654
|
Dissolved Aluminum
|
pH < 6.0
|
log(Al) = -0.925pH + 4.851
|
0.429
|
pH > 6.0
|
Al = 0.2 mg/L
|
Dissolved Arsenic
|
|
< 0.2 mg/L
|
0
|
Dissolved Cadmium
|
pH < 3.0
|
Cd = 0.07 mg/L
|
0
|
pH > 3.0
|
Cd = 0.015 mg/L
|
Dissolved Calcium
|
|
log(Ca) = +0.619log(SO4) + 0.524
|
0.375
|
Dissolved Copper
|
pH < 3.4
|
log(Cu) = -1.485pH + 6.605
|
0.692
|
3.4<pH<5.4
|
log(Cu) = -0.327pH + 2.666
|
pH > 5.4
|
log(Cu) = -1.001pH + 6.307
|
Total Copper
|
|
log(CuT) = +0.962log(CuD) + 0.180
|
0.23
|
Dissolved Iron
|
pH < 4.4
|
log(Fe) = -1.429pH + 6.286
|
0.807
|
pH > 4.4
|
log(Fe) = -0.455pH +2.000
|
Total Iron
|
|
If diss Fe>1.0, total Fe=diss Fe
|
0
|
Dissolved Lead
|
|
Pb = 0.05 mg/L
|
0
|
Dissolved Nickel
|
|
log(Ni) = -0.317pH + 0.853
|
0.607
|
Total Nickel
|
|
total Ni = diss Ni
|
0.613
|
Dissolved Selenium
|
|
Se = 0.2 mg/L
|
|
Dissolved Silver
|
|
Ag = 0.015 mg/L
|
|
Dissolved Zinc
|
|
log(Zn) = -0.441pH + 1.838
|
0.667
|
Total Zinc
|
|
total Zn = diss Zn
|
0.144
|
The seasonal fluctuations in equilibrium concentrations are caused by natural processes like
temperature variations, as well as artificial factors like analytical error and filtration effects. Each
factor contributes to the standard deviation based on its weighting factor:
(log standard deviation)2 = weightfactor1*variationfactor1 + weightfactor2*variationfactor2 + ... (Eq. 4)
In a complex open system like a minesite, the weighting factors and variations of all significant
factors cannot be identified. So, while Equation 4 mathematically explains the source of the
seasonal variability of equilibrium concentrations, the standard deviation remains an empirically
observed site-specific value.
EDCMs allow estimates of variable concentrations over very short periods that may not have
been monitored. For example, with dissolved copper at pH 5.0 in Table 1, the average annual
equilibrium concentration is:
log(avg. annual copper, mg/L) =
= -0.327pH + 2.666 (Eq. 5)
= -0.327*5.0 + 2.666
= +1.03
Average annual equilibrium copper = 10.7 mg/L
Standard probability tables applied to one year indicate the maximum equilibrium
concentration of one-week duration would be 2.34 log standard deviations above the average annual
equilibrium concentration (best-fit line). Thus, the corresponding maximum one-week-duration
concentration of dissolved copper at pH 5.0 is:
log(max. one-week-duration copper) =
= -0.327pH + 2.666 + (2.34*0.692) (Eq. 6)
= -0.327*5.0 +2.666 + (2.34*0.692)
= +2.65
Maximum one-week-duration equilibrium copper each year = 447 mg/L
As explained earlier, equilibrium concentrations reflect site-specific factors, and thus can
deviate from globally expected levels derived from stock mineral solubility or other global
characteristics. A compilation of EDCMs for 15 minesites and minesite components showed that
average annual equilibrium copper concentrations were quantitatively unique to each minesite, but
followed similar qualitative patterns with pH (Figure 16; Morin et al., 2001). Depending on pH,
average-annual equilibrium copper concentrations among the sites differed by up to three orders of
magnitude (Figure 17). Furthermore, for eight months each year, equilibrium copper concentrations
statistically remained within plus-and-minus one standard deviation of the annual average. This was
a total span of one order of magnitude (a factor of 10) for the average site, but varied from 0.4 to 1.6
orders of magnitude among the sites (Figure 17). For four months every year, concentrations were
outside (above and below) this span around the annual average. Similar observations were made for
zinc, lead, and nickel.

Figure 16. Average Annual Equilibrium Copper Concentrations vs. pH
from Empirical Drainage Chemistry Models of Fifteen Minesites and
Minesite Components.

Figure 17. Average Annual Equilibrium Copper Concentrations (horizontal
lines) and Ranges of Seasonal Equilibrium Copper Concentrations
(vertical lines representing one logarithmic standard deviation) at pH
3.5 from Empirical Drainage Chemistry Models of Fifteen Minesites
and Minesite Components.
Therefore, equilibrium concentrations can vary seasonally, sometimes by more than one
order of magnitude. However, average annual equilibrium concentrations remain about the same
year after year, if pH and other master parameters remain constant. In Figure 4, very low seasonal
concentrations may appear as a trend to the left of the scale transition, into kinetic conditions. While
this may sometimes be true, a repeating seasonal variation would suggest the variable concentrations
are actually in equilibrium and remain to the right of the scale transition. Nevertheless, there can
be some confusion for sites near the scale transition, where highly variable concentrations may
reflect both equilibrium and kinetically controlled conditions.
8. Conclusion
Based on the discussions and findings of this MDAG case study, some of the more important
points for scaling of minesite-drainage chemistry were:
- “Many people say they already know how to scale minesite-drainage chemistry, but no one
actually understands scaling well.”
- Physical aspects like water flowpaths, sequences of minerals, and sampling location affect
drainage chemistry on all scales.
- Mesoscale analyses like acid-base accounting and laboratory kinetic tests implicitly predict
homogenized conditions, whereas full-scale minesite components are too large relative to
humans to be considered homogeneous.
- “Equilibrium” encompasses thermodynamic equilibrium, metastable equilibrium, dynamic
equilibrium, pseudo-equilibrium, and emergence. As scaling factors like volume, rate,
residence time, and solid:liquid ratio increase, aqueous concentrations eventually reach a
maximum equilibrium level and rise no higher.
- The “scale transition”, marking the break between kinetically determined and equilibrium
determined concentrations, can involve less than a kilogram or more than thousands of
tonnes of rock or tailings. Corresponding vertical heights can be roughly centimeters to tens
of meters.
- Sometimes a 1 kg humidity cell can provide equilibrium concentrations, in mg/L, equivalent to
full-scale levels. This occurs for elements whose kinetic rate is high and equilibrium
concentration is relatively low. In these cases, equilibrium concentrations should not be
converted to rates for predictions of lag times and NPR criteria.
- The accumulation of secondary minerals under equilibrium conditions can greatly extend the time
that equilibrium is maintained. This is due to subsequent dissolution of the accumulated
minerals.
- Full-scale equilibrium does not mean only one constant concentration throughout the year.
Empirical Drainage Chemistry Models (EDCMs) with thousands of analyzes spanning many
years to decades showed that seasonal variations in equilibrium concentrations could exceed
one order of magnitude. As long as “master” parameters like pH remain relatively constant,
the average-annual equilibrium concentrations and their seasonal variability will also remain
constant, but unique for each element at each minesite.
9. References
Anderson, P.W. 1972. More is different: Broken symmetry and the nature of the hierarchical
structure of science. Science 177, p. 393-396.
Beckie, R., L. Smith, K. Wagner, and F. Guerin. 2005. Geochemistry of an Experimental Waste
Rock Pile, Cluff Lake, Saskatchewan: Comparison of Lab Scale and Field Scale Weathering
Rates. In: Proceedings of the 12th Annual British Columbia MEND ML/ARD Workshop
(Vancouver, Canada, November 30 - December 1).
Day, S.D., T. Higgs, and M. Paine. 1996. Guide for Predicting Water Chemistry from Waste Rock
Piles. Canadian MEND Report 1.27.1a, July 1996.
Dinardo, O. 2003. Thiosalts in the mining industry? A review of the projects funded by the
Thiosalts Consortium. In: Proceedings of Sudbury 2003, Mining and the Environment
(Sudbury, Canada, May 25-28, 2003).
Garvie, A.M., J.W. Bennett, and A.I.M. Ritchie. 1997. Quantifying the spatial dependence of the
sulfide oxidation rate in a waste rock dump at Mt Lyell, Tasmania. p.335-349. In:
Proceedings of the Fourth International Conference on Acid Rock Drainage, Volume I
(Vancouver, Canada, May 31 to June 6, 1997).
Hanna, G.P. and R.A, Brant. 1962. Stratigraphic relations to acid mine water production. In:
Proceedings of the 17th Industrial Waste Conference, Series No. 112, Engineering Extension
Series, Purdue University.
Hornberger, R.J. and K.B.C. Brady. 1998. Chapter 7 - Kinetic (Leaching) Tests for the Prediction
of Mine Drainage Quality. Coal Mine Drainage Prediction and Pollution Prevention in
Pennsylvania. The Pennsylvania Department of Environmental Protection,
http://www.dep.state.pa.us/dep/deputate/minres/districts/cmdp.
Jansen, M. and A. Taylor. 2002. A new approach to heap leach modelling and scale-up. In:
Proceedings of the ALTA Copper-7 Conference. http://www.altamet.com.au/
Technical%20Papers%20and%20Articles/ALTA%20Copper/New%20Approach%20to%20Heap%20Leach%20Modelling%20and%20Scale-Up.pdf.
Jones, C.A., D.A. Nimick, and R.B. McCleskey. 2004. Relative effect of temperature and pH on
diel cycling of dissolved trace elements in Prickly Pear Creek, Montana. Water, Air, and
Soil Pollution, 153, p. 95-113
Kempton, J.H., D. Swanson, M. Bennett, R. MacDonald, W. Locke, C. Gillespie, M. Lechner, and
P. Maley. 1997. Application of probabilistic acid/base accounting to minimize waste-rock
handling in semi-arid climates. p.871-888. In: Proceedings of the Fourth International
Conference on Acid Rock Drainage, Volume II (Vancouver, Canada, May 31 to June 6,
1997).
Kuo, E.Y., and A.I.M Ritchie. 1999. The impact of convection on the overall oxidation rate in
sulfidic waste rock dump. p. 211-220. In: D. Goldsack, N. Belzile, P. Yearwood, and G.
Hall, eds., Proceedings of Sudbury '99, Mining and the Environment II (Sudbury, Canada,
September 13-17).
Li, M. 1999. Hydrology and Solute Transport in Oxidised Waste Rock from Stratmat Site, N.B.
Canadian MEND Report 2.36.2b.
Li, L., C.A. Peters, and M.A. Celia. 2006. Upscaling geochemical reaction rates using pore-scale
network modelling. Advances in Water Resources, 29, p. 1351-1370.
Mehling, P.E., S.J. Day, and K.S. Sexsmith. 1997. Blending and layering waste rock to delay,
mitigate or prevent acid generation: A case study review. p.951-969. In: Proceedings of the
Fourth International Conference on Acid Rock Drainage, Volume II (Vancouver, Canada,
May 31 to June 6, 1997).
Morin, K.A. 2003. Problems with acid rock drainage predictions at the Ekati Diamond Mine,
Northwest Territories, Canada. p. 663-670. In: T. Farrell and G. Taylor, eds., Proceedings
from the Sixth International Conference on Acid Rock Drainage (Cairns, Australia, July
14-17). The Australian Institute of Mining and Metallurgy.
Morin, K.A. 1994. Prediction of water chemistry in open pits during operation and after closure.
IN: Proceedings of the Eighteenth Annual British Columbia Mine Reclamation Symposium,
Vernon, British Columbia, April 11-14, p. 72-86.
Morin, K.A., and N.M. Hutt. 2007. Errors from sampling humidity cells every second week.
MDAG Internet Case Study #24, www.mdag.com/case_studies/cs24.html.
Morin, K.A., and N.M. Hutt. 2006a. Rock grain size and its implications for minesite-drainage
chemistry. MDAG Internet Case Study #23, www.mdag.com/case_studies/cs23.html.
Morin, K.A. and N.M. Hutt. 2006b. Case studies of costs and longevities of alkali-based
water-treatment plants for ARD and minesite-drainage chemistry, and their implications on
net-present-value estimates. In: Proceedings of the 7th International Conference on Acid
Rock Drainage (these proceedings, March 26-30, 2006, St. Louis, MO, USA).
Morin, K.A., and N.M. Hutt. 2001. Environmental Geochemistry of Minesite Drainage: Practical
Theory and Case Studies - Digital Edition. MDAG Publishing (www.mdag.com), Surrey,
Canada. ISBN 0-9682039-1-4.
Morin, K.A., and N.M. Hutt. 2000a. Discrete-zone mixing of net-acid-neutralizing and
net-acid-generating rock: Avoiding the argument over appropriate ratios. p. 797-803. In:
Proceedings from the Fifth International Conference on Acid Rock Drainage, Volume II
(Denver, USA, May 20-26, 2000). Society for Mining, Metallurgy, and Exploration, Inc.,
Littleton, CO, USA.
Morin, K.A., and N.M. Hutt. 2000. Case studies in metal solubility at minesites. Presented at the
7th Annual British Columbia Metal Leaching/ARD Workshop, Vancouver, November 29-30.
Morin, K.A. and N.M. Hutt. 1999. Onset of acidic drainage from a mine-rock pile. MDAG
Internet Case Study 11 at www.mdag.com/case_studies/cs3-99.html.
Morin, K.A., and N.M. Hutt. 1998a. Minesite drainage chemistry is like rain. MDAG Internet Case
Study #3, www.mdag.com/case_studies/cs1-98.html.
Morin, K.A., and N.M. Hutt. 1998b. Motherhood, apple pie, and contaminant source reduction.
MDAG Internet Case Study #7, www.mdag.com/case_studies/cs7-98.html.
Morin, K.A., and N.M. Hutt. 1998c. Kinetic tests and risk assessment for ARD. The 5th Annual
British Columbia Metal Leaching and ARD Workshop, December 9-10, Vancouver, British
Columbia, Canada, B.C. Ministry of Energy and Mines and MEND 2000.
Morin, K.A., and N.M. Hutt. 1997. Environmental Geochemistry of Minesite Drainage: Practical
Theory and Case Studies. MDAG Publishing (www.mdag.com), Surrey, Canada. ISBN 0-9682039-0-6.
Morin, K.A., and N.M. Hutt. 1993. The use of routine monitoring data for assessment and
prediction of water chemistry. IN: Proceedings of the 17th Annual Mine Reclamation
Symposium, Port Hardy, British Columbia, May 4-7, p.191-201. Mining Association of
British Columbia.
Morin, K.A., N.M. Hutt, and S. Hutt. 2001. A compilation of empirical drainage-chemistry models
(EDCMs). IN: Proceedings of Securing the Future, International Conference on Mining and
the Environment, Skellefteå, Sweden, June 25-July 1, Volume 2, p. 556-565. The Swedish
Mining Association.
Morin, K.A., N.M. Hutt, and I.A. Horne. 1995a. Prediction of future water chemistry from Island
Copper Mine's On-Land Dumps. IN: Proceedings of the 19th Annual British Columbia
Mine Reclamation Symposium, Dawson Creek, B.C., June 19-23, p. 224-233.
Morin, K.A., N.M. Hutt, and R. McArthur. 1995b. Statistical assessment of past water chemistry
to predict future chemistry at Noranda Minerals' Bell Mine. IN: Proceedings of the
Conference on Mining and the Environment, Sudbury, Ontario, May 28 - June 1, Volume
3, p.925-934.
Morin, K.A., I.A. Horne, and D. Flather. 1993. The appropriate geochemical monitoring of toe
seepage from a mine-rock dump. IN: Proceedings of the 17th Annual Mine Reclamation
Symposium, Port Hardy, British Columbia, May 4-7, p.119-129. Mining Association of
British Columbia.
Petrunic, B.M. and T.A. Al. 2005. Mineral/water interactions from a tungsten mine, Mount
Pleasant, New Brunswick. Geochimica et Cosmochimica Acta, 69, p. 2469-2483.
Ritchie, A.I.M. 1995. Application of oxidation rates in rehabilitation design. p. 101-116. In: N.J.
Grundon and L.C. Bell, eds., Proceedings of the Second Australian Acid Mine Drainage
Workshop (Charter Towers, Queensland, Australia, March 28-31).
Shope, C.L., Y. Xie, and C.H. Gammons. 2006. The influence of hydrous Mn–Zn oxides on diel
cycling of Zn in an alkaline stream draining abandoned mine lands. Applied Geochemistry,
21, p. 476-491.
Wu, J. 1999. Hierarchy and scaling: Extrapolating information along a scaling ladder. Canadian
Journal of Remote Sensing, 25, p. 367-380.
Wu, J., and H. Li. 2006. Chapter 1: Concepts of Scale and Scaling. IN: J. Wu, H. Li, and O.L.
Loucks, eds., Scaling and Uncertainty in Ecology: Methods and Applications, p. 3-15,
Springer, Netherlands.
© 2007 Kevin A. Morin and Nora M. Hutt
For more case studies, see Environmental Geochemistry of Minesite
Drainage: Practical Theory and Case Studies.
Home • Up
Created by K.Morin
















